先前一篇博文(如何保持空域与频域滤波结果的一致性)中谈到,从空域小模板转化到频域滤波时,为了保持空频滤波的一致性,需要合理处理空域滤波器的延拓和布局问题。一般做法是,将小模板的中心通过循环移位后置于补零延拓矩阵的左上角。然后做傅里叶变换,得到对应的频域滤波器,再与延拓后的图像在频率域与滤波器做乘法运算。具体的原理和方法可参看前述博文。
设有一幅M×N的图像f(x,y),m×n的空域滤波器为h(x,y),则频域滤波的处理步骤如下:
(1) 消除折叠现象的填充(Zero padding)。即分别对f(x,y),h(x,y)的右下部补零至P×Q得到fp(x,y)和hp (x,y),其中h(x,y)需要做循环移位,以使小模板h(x,y)的中心像素置于hp (x,y)的左上角。一般取:P=2M,Q=2N 。
(2) fp(x,y),hp (x,y)分别做傅里叶变换产生Fp(u,v),Hp(u,v)。
(3) 中心变换(频谱中心化)。此步也可以不变换,则Hp(u,v)要改变(针对直接在频域生成对称滤波器情况)。
(4) 频域滤波:Hp(u,v)点乘Fp(u,v)。
(5) 傅里叶反变换。
(6) 取实数部分。绝对值很小的虚数部分是浮点运算存在误差造成的。
(7) 空域中心还原变换(反中心化)。若Fp(u,v)未做中心化,此步可省。
(8) 截取有效数据,即左上角的原始图像尺寸M×N部分数据。
以上步骤的滤波,仅限于空域滤波的边界处理为零填充方式。如果空域滤波的边界处理为其他方式,如对称边界('symmetric')重复边界('replicate')和周期边界('circular')等,则依然会存在空频域滤波结果在边界上的差异性。如图1所示,是一个方差为4的25×25高斯低通滤波器对cameraman图像分别在空域和频域滤波结果的对比。可以看出,频域滤波与空域滤波在边界上是不一致的。

图1 仅在空域考虑了边界因素的滤波结果
那么,如何有效解决这个问题呢?其实也很简单,只要在步骤(1)和(8)上稍稍改进,就可以保持空/频域滤波结果边界上的一致性。
第(1)步,根据h(x,y)的尺寸对f(x,y)先做重复边界的扩充,在此基础上做消除折叠的补零延拓,即得到扩大至(2M+行重复边界数)×(2N+列重复边界数)的fp(x,y),如图2所示。对h(x,y)右下部补零至与fp(x,y)的相同尺寸,并循环移位后得到hp (x,y)。
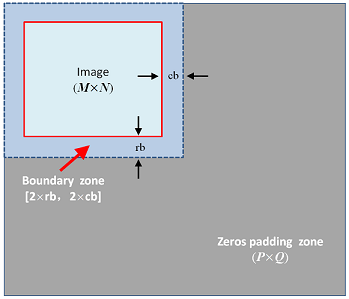
图2 滤波前图像边界扩充及补零延拓
第(8)步,截取有效数据时,应除去左上角单边边界数后的原始图像尺寸(M×N)部分数据(即图2中的红框区域)。其他步骤不变,即可得到与空域滤波完全一致的结果,如图3所示。

图3 空频域等效边界模式的滤波结果
MATLAB参考代码如下:
%=============================================================================
inimg = imread('cameraman.tif');
subplot(131)
imshow(inimg), title('Original image')
[M,N] = size(inimg); % Original image size
%====================================================================
h = fspecial('gaussian',25,4); % Gaussian filter
%====================================================================
% 空域滤波
gx = imfilter(inimg,h,'same','replicate'); % 空域图像滤波
subplot(132)
imshow(gx,[]);title('Spatial domain filtering')
%====================================================================
% 频域滤波
%====================================================================
h_hf = floor(size(h)/2); % 空域滤波器半高/宽
imgp = padarray(inimg, [h_hf(1),h_hf(2)],'replicate'); % Padding boundary with copying pixels
% PQ = paddedsize(size(imgp)); % Gonzalez DIP教材提供的函数,非MATLAB内部函数
PQ = 2*size(imgp);
Fp = fft2(double(imgp), PQ(1), PQ(2)); % 延拓图像FFT
% h = rot90(h,2); % Mask旋转180度,非对称h需此步骤!因频域乘积对应空域卷积,而空域滤波为相关。
P = PQ(1); Q = PQ(2);
center_h = h_hf+1; % 空域小模板h中心位置
hp = zeros(P,Q); % 预分配内存,产生P×Q零矩阵
hp(1:size(h,1),1:size(h,2)) = h; % h置于hp左上角
hp = circshift(hp,[-(center_h(1)-1),-(center_h(2)-1)]); % 循环移位,h中心置于hp左上角
%====================================================================
Hp = fft2(double(hp)); % hp滤波器做FFT
%====================================================================
Gp = Hp.*Fp; % 频域滤波
gp = real(ifft2(Gp)); % 反变换,取实部
gf = gp(h_hf(1)+1:M+ h_hf(1), h_hf(2)+1:N + h_hf(2)); % 截取有效数据
subplot(133)
imshow(uint8(gf),[]), title('Frequency domain filtering')
% 注:以上处理中,频域图像Fp与滤波器Hp均未中心化,因此,返回空域时无需反中心化。
% 另外,直接调用Hp = freqz2(h,P,Q)获得的2D频域响应,则是中心化的。
代码下载:mySFFilt2Demo.m


扫一扫,可关注“老马迷图”微信公众号!
相关博文:如何保持空域与频域滤波结果的一致性