相关性,是指两个变量的关联程度。一般地,从散点图上可以观察到两个变量有以下三种关系之一:两变量正相关、负相关、不相关。如果一个变量高的值对应于另一个变量高的值,相似地,低的值对应低的值,那么这两个变量正相关。反之,如果一个变量高的值通常对应于另一个变量低的值,那么这两个变量负相关。如果两个变量间没有关系,即一个变量的变化与对应的另一变量的变化之间没有明显关系,那么这两个变量不相关。
因果性描述的是两个事件之间的作用关系,其中第一个事件被称为“因”,第二个事件被称为“果”,第二个事件的发生全部或者部分依赖于第一个事件的发生,而且第一个事件的发生在时间上必须严格早于第二个事件。如果用统计的语言来说,如果两个变量之间存在因果关系,则第二个变量(果)的取值全部或者部分依赖于第一个变量(因)的取值。
衡量相关性的指标很多,常见的有Pearson相关性、Spearman排序相关性、Kendall排序相关性等等[1],从数据中可以直接得到并且不会带来任何本质上的误解。与之相对,要说明两个变量之间存在因果性,如果仅仅从数据出发,是非常困难的,因为没有办法说明这两个变量之间的关系不是通过其他中介变量实现的,比如Y因为X的变化而变化,有可能不是X直接作用于Y,而是存在某个Z,Z同为X和Y的原因,但是X响应Z的变化比Y更快。
随着大数据关联分析和深度学习等工具的流行,我们变得越来越少谈论因果。在大多数时候,我们将输入的数据一股脑喂进装着神经网络的黑匣子的一端,在黑匣子外面,我们只能听到神经网络的咀嚼声,然后就是从另一端淅淅沥沥落下来的预测结果。在少数更好的场景中,相关的变量足够少且意义清晰,使得我们可以讨论两个或者多个变量之间的相关性。至于因果,则是一件公认的危险玩意儿,我们一般缄口不谈,即便谈到了也是晦涩审慎,在它身边堆满了“暗示”、“可能”、“潜在”等等还没有上战场,就已经举白旗的投降词汇。这是因为,尽管因果分析是一个重要和热门的研究方向,但迄今为止我们依旧缺乏一套在数学上可靠且行之有效的处理因果的方法和工具,或者说目前的数学工具需要的前提条件往往超过了真实数据采集场景所能给予的[2]。
那么,在人类认识世界的过程中,“因果”是一个稀罕物吗?恰恰相反,在绝大多数时间,因果是我们认识世界的手段和目的——我们坚信万事万物的存在、运动和转化都是有原因的,并且习惯用已知的因果关系推导未知的因果关系。且不说牛顿定律、量子力学、化学反应方程式、遗传定律等等可以表述为因果的科学理论,就算是亚里士多德的四因说(形式因、质料因、动力因、目的因)和“力是维持物体运动的原因”、托勒密的地心说等已经被抛弃的学说,以及各种并不科学的竞合的宗教教义,都没有超出因果的框架。可以说,在很长一个阶段,人类的科学史甚至整个思想史,都是因果推出因果,因果战胜因果的历史。
我们得到可信的因果关系,有两条主要的途径。一是基于一些公认的公理、原理和推导方法,以及从以上公理和推导方法已经获得的可验证的定理,得到的因果关系。例如赫兹1887年就发现了著名的光电效应,即在高于某特定频率的光的照射下,金属表面可以逸出电子并形成电流,即光生电。而且,单个逸出电子的最大动能是和光的频率正相关,但与光照的时间长短并无关系。这个时候我们只能说逸出电子的最大动能和照射光频率之间是相关的,还不能妄谈两者之间的因果关系。到了1905年,基于光的粒子说和普朗克提出的朴素的量子原理,爱因斯坦给出了光电效应的科学解释和光电效应公式,我们才能认为照射光的频率和逸出电子的最大动能之间存在因果关系,前者为因,后者为果。后者也不完全由前者决定,因为金属的材质决定了极限频率,而这个值也会影响逸出电子的最大动能。后来随着越来越多的实验验证了爱因斯坦光电效应公示的合理性,两者之间的因果性就变得越来越可信。二是通过精细设计的实验,控制掉可能的影响因素,获得对因果关系的验证。例如,为了证明服用某种药物(事件A,因事件)与治疗某种疾病(事件B,果事件)之间存在因果关系,可以将身体和病程发展情况相近的足够多的病人随机分为两组,其中一组服用待测试的药物,另外一组服用安慰剂,然后分析两组病人病程发展的情况,对比分析服用药物是否会带来效果。一般而言,我们要求试验人员和被试病人都不知道谁服用了药物谁服用了安慰剂,因此被称为“双盲实验”;在更严格的要求下,我们还要求第三方做分析,并且分析人员也不知道所得到的两组数据哪一组来自于服用药物的,哪一组来自于服用安慰剂的,这被称作“三盲实验”。社会学和心理学的很多实验也采用了类似的方法论,如果严格按照该方法设计并且数据样本足够多也足够有代表性,我们一般认为所得到的因果关系是比较可信的。
读者要意识到,因果关系没有100%可信的,因为第一性原理的推导也有可能藏有错误,而可控实验通常也无法完美地控制所有可能相关的因素。如果把科学看作发现因果关系的过程,那么因果关系能够被信赖的一个关键特征就是它是潜在不可信赖的,或者说是可证伪的[3]。与之相对,对于某些变量对,我们可以断言两者的相关性是100%成立的,不过是或大或小罢了。
正是因为相关性确凿无疑,而因果性充满风险,基于相关性的分析和应用成为了调查分析人员的新宠。基于真实的数据,采用“暴力”的关联分析方法(例如回归分析)和预测算法(例如深度学习),我们可以观察到数据之间的相关性,还能得到“相当可信”的预测结果。尽管这些都不会增加对于系统运行机制坚实的理解,但对于一些浅层次的应用而言,这似乎已经足够了。这些暴力手段一度让我们迷失,以至于十年前迈尔-舍恩伯格在具有全球影响力的《大数据时代》一书[4]中呐喊“大数据时代需要放弃对于因果关系的渴望,而只需关注相关关系”。
过度依赖相关性的主要风险来源于现代人类难以克服的幻觉:不由自主地把相关当成因果来对待。这会带来两个实际的风险:一是错误的预测,二是无效的干预。
先谈谈错误的预测。我们从“利用搜索数据预测流感传播情况”这个著名的例子说起。流感样疾病(ILI)暴发的实时预测通常由于难以及时收集和分析大量数字数据而受阻。传统的监测依赖于收集临床医生的记录和医疗索赔数据,受限于数据覆盖、空间分辨率和交付分析结果的长期延迟[5]。信息技术的进步使收集与公共健康有关的大规模搜索查询数据成为可能,这使得很多研究人员开始关注如何用搜索查询数据预测ILI的传播情况[6]。这些工作的灵感起源于Eysenbach发现的一个重要的相关性:2004-2005年加拿大流感季中,在谷歌中输入“flu”或“flu symptoms”后得到的链接所获得的点击次数与流感感染人数密切相关,其Pearson相关性高达0.91[7]。受到Eysenbach所观察到的相关性的启发,谷歌于2008年推出了基于互联网的流感监测工具Google Flu Trends(GFT),该工具使用汇总的谷歌搜索数据以实时估计流感病毒的活动。进一步地,Ginsberg等人[8]分析了带有流感样症状的谷歌搜索查询数据,并提出了一种方法,可以预测(估计)美国每个地区每周流感活动的当前水平。显然,一个人很可能因为出现在流感症状而在Google上搜索相关信息,但几乎不可能因为打开了Google搜索框而染上流感。实际上,我们可以把大量的相关搜索(X)和疾控中心报告的病例增长(Y)都看作流感肆虐(Z)的结果。也就是说,我们观察到的X和Y的相关实际上来源于X和Y都是同一个原因Z的结果。如果X和Y完完全全只依赖于Z,那么用X预测Y在实践上是安全的,因为X和Y都可以写成只含有Z的函数:X=f(Z)和Y=g(Z)。如果f和g已知且f可逆,那么Y可以唯一表示为Y=g(f-1(X)),如果这些条件不能显式的满足,我们显然也可以通过大量真实数据拟合得到近似的函数。遗憾的是,真实复杂系统中很少有完完全全的依赖关系,在这个典型的例子中,流感肆虐的情况并不能完全决定搜索相关信息的频繁程度,事实上,有一些充满好奇心的技术极客在看了文献[8]之后,写了一些自动搜索相关信息的脚本程序(Q),从而让搜索量大幅度上升,导致基于相关性的预测算法出现错误。之所以预测出现错误,是因为X不仅仅由Z决定,还可能受到Q或者其他因素的影响,所以公式Y=g(f-1(X))在Q发生变化后,就变得荒谬。一些学者也及时发现了这些问题,如Olson等人[9],Lazer等人[10]都从数据有效性、可靠性和算法的动态性等方面提出了对文献[8]所报告算法的质疑。以前有欧洲的团队利用Twitter上针对某些股票情绪的变化来预测股价的变化,并藉此获利,但很快就有对手方故意通过机器粉丝发表针对目标股票带有情绪化和倾向性的言论,干扰算法的判断并反向套利。这些风险都是因为过度相信没有直接因果关系的相关性。
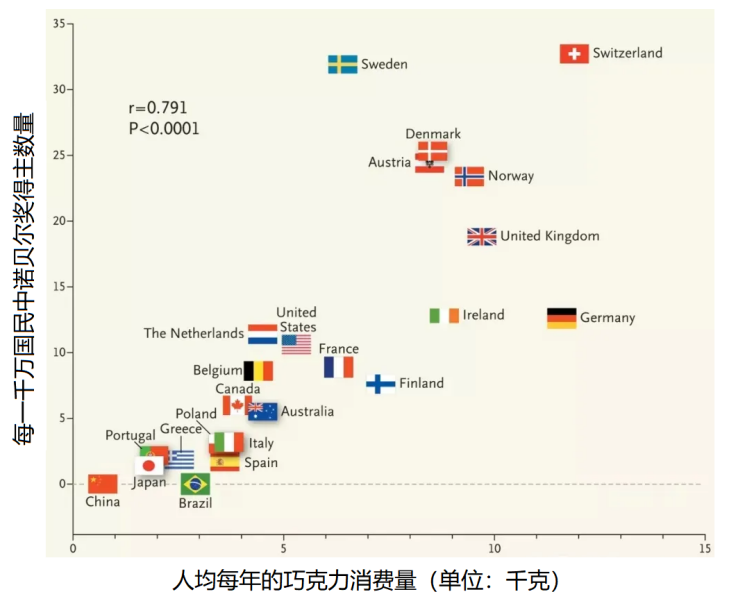
图1:一个国家的人均诺贝尔奖得主数量和人均每年巧克力消费量之间的关系。两者表现出显著的正相关,Pearson相关性高达0.791。
再说说无效的干预。由于我们不由自主会把相关性当作因果性来对待,所以当我们着眼于改变Y,而又发现了X和Y的相关性后,我们就会自然地想通过干预X来改变Y。2012年,著名的《新英格兰医学杂志》刊登了一篇传播极广又饱受诟病的论文“巧克力消费量,认知能力和诺贝尔奖得主”[11],该文分析了若干国家每一千万公民中诺贝尔奖得主的人数与平均每个公民一年巧克力消费量的相关图(如图1所示),发现这两者具有显著的正相关性,其Pearson相关性高达0.791。文章还专门指出瑞典之所以明显偏离了线性关系,是因为诺贝尔奖就是他们颁的,他们不够客观。从图中可以看到,欧美人很喜欢巧克力,其人均消费量是中国的几倍甚至十余倍。那么,中国是不是从中找到了赶超欧美的快车道——大力发展巧克力产业并鼓励人民消费巧克力?遗憾的是,这条路似乎是行不通的,因为这篇文章很快就成了众多统计学家和经济学家茶余饭后的笑柄,事实上,陆续有大量的批评论文发表,这些文章举出了很多讽刺的例子,比如发现牛奶消费量[12]、宜家商店数量[13]等等都和诺贝尔奖得主数高度相关。如果我们过度相信相关性,通过新修大量宜家商店,并且鼓励巧克力和牛奶的消费,以求一跃成为诺贝尔奖的常客,会成功吗?显然不会!
我们着重描述了应用相关性潜在的风险,并不是要否定相关性——实际上这依然是绝大部分多变量定量分析中最强大的工具,只是希望大家在应用中减少误解和错误。另外,相关性并不是因果性的敌人,实际上它们是紧密的战友,因为发现相关性往往能够提示可能的因果关系。
参考文献:
[1] G. R. Iversen, M. Gergen, Statistics: The Conceptual Approach, Springer, 1997.
[2] 朱迪亚·珀尔,( 刘礼 、杨矫云、廖军、李廉译),《因果论:模型、推理和推断》,机械工业出版社,2022。
[3] 卡尔·波普尔,(查汝强 / 邱仁宗 / 万木春),《科学发现的逻辑》,中国美术学院出版社,2008.
[4] 维克托·迈尔-舍恩伯格,肯尼斯·库克耶,(盛杨燕、周涛译),《大数据时代:生活、工作与思维的大变革》,浙江人民出版社,2012。
[5] E. C. Lee, A. Arab, S. M. Goldlust, C. Viboud, B. T. Grenfell, S. Bansal, Deploying digital health data to optimize influenza surveillance at national and local scales, PLoS Computational Biology 14 (2018) e1006020.
[6] M. Santillana, E. O. Nsoesie, S. R. Mekaru, D. Scales, J. S. Brownstein, Using clinicians’ search query data to monitor influenza epidemics, Clinical Infectious Diseases 59 (2014) 1446-1450.
[7] G. Eysenbach, Infodemiology: Tracking flu-related searches on the web for syndromic surveillance, in: AMIA Annual Symposium Proceedings, 2006, pp. 244-248.
[8] J. Ginsberg, M. H. Mohebbi, R. S. Patel, L. Brammer, M. S. Smolinski, L. Brilliant, Detecting influenza epidemics using search engine query data, Nature 457 (2009) 1012-1014.
[9] D. R. Olson, K. J. Konty, M. Paladini, C. Viboud, L. Simonsen, Reassessing Google Flu Trends data for detection of seasonal and pandemic influenza: A comparative epidemiological study at three geographic scales, PLoS Computational Biology 9 (2013) e1003256.
[10] D. Lazer, R. Kennedy, G. King, A. Vespignani, The parable of Google Flu: Traps in big data analysis, Science 343 (2014) 1203-1205.
[11] H. Franz, M. D. Messerli, Chocolate Consumption, Cognitive Function, and Nobel Laureates, The New England Journal of Medicine 367 (2012) 1562-1564.
[12] S. Linthwaite, G. N. Fuller, Milk, chocolate and Nobel prizes, Practical Neurology 13 (2013) 66.
[13] P. Maurage, A. Heeren, M. Pesenti, Does Chocolate Consumption Really Boost Nobel Award Chances? The Peril of Over-Interpreting Correlations in Health Studies, The Journal of Nutrition 143 (2013) 931-933.