图像处理及机器视觉应用中的Sobel算子,是以它的提出者Irwin Sobel名字命名的。该算子没有在任何期刊或会议上正式发表过,当时仅在Stanford大学人工智能项目组的一个非正式的博士生讨论组会上与Gary Feldman(当时的一个在读研究生,也是Sobel的朋友)共同提出。Irwin Sobel还曾专门撰文申明,建议把Sobel算子的命名改成“Sobel-Feldman”算子[1-2]。
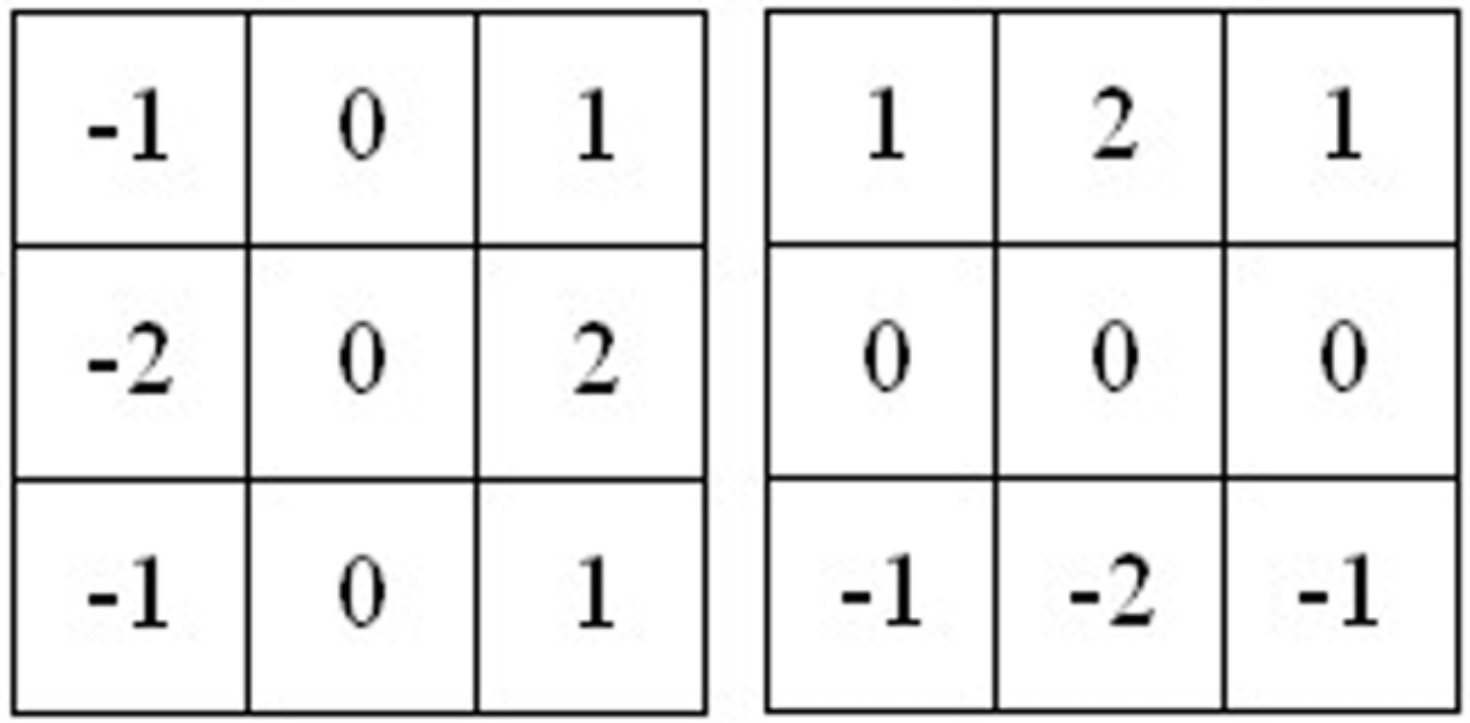
图1 Sobel算子(滤波模板)
对于这个看似简单却沿用了几十年的算子,包括国际上最流行的冈萨雷斯《数字图像处理》教材在内,很多教科书并没有对算子的原理和数学基础做具体描述。
Sobel算子考虑了水平、垂直和2个对角共计4个方向对的梯度加权求和,是一个3×3各向异性的梯度算子。另外,大部分教科书停留在对算子的直观解释上,一般描述为隔行或隔列的差分运算,然后做中心像素位置的2倍加权。实际上,并不是现行教科书上描述的简单的隔行/列的差分运算,中心像素位置也并未参与运算(N8(p)邻域,非3×3邻域)。
Sobel算子具有严格的数学基础,主要关键点在于:
1)笛卡尔网格(Cartesian grid);
2)前向差分(Forward-difference);
3)距离反比的4方向对梯度加权;
4)城市距离(City-block distance)。
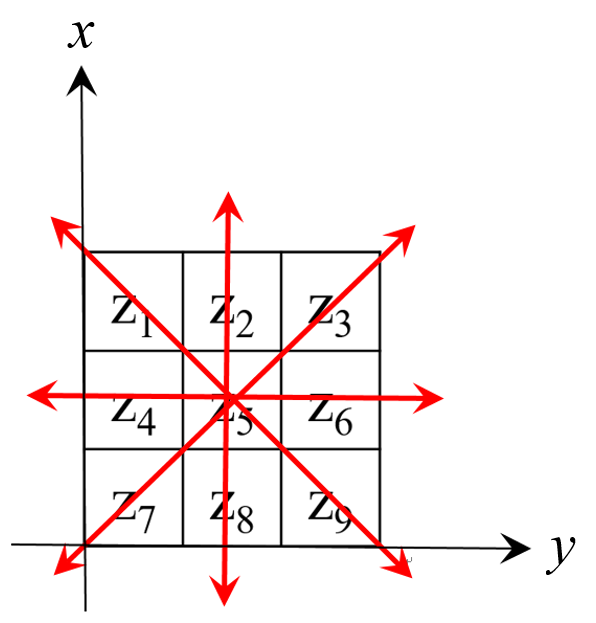
图2 像素N8(p)邻域及Cartesian网格
定义一个给定邻域方向梯度矢量g的幅度为
|g| = <像素灰度差分>/<相邻像素的距离>
Sobel采用的像素距离是一种城市距离(city-block),而并非通常的欧式距离。因此,对角方向相邻像素之间的距离值为2。
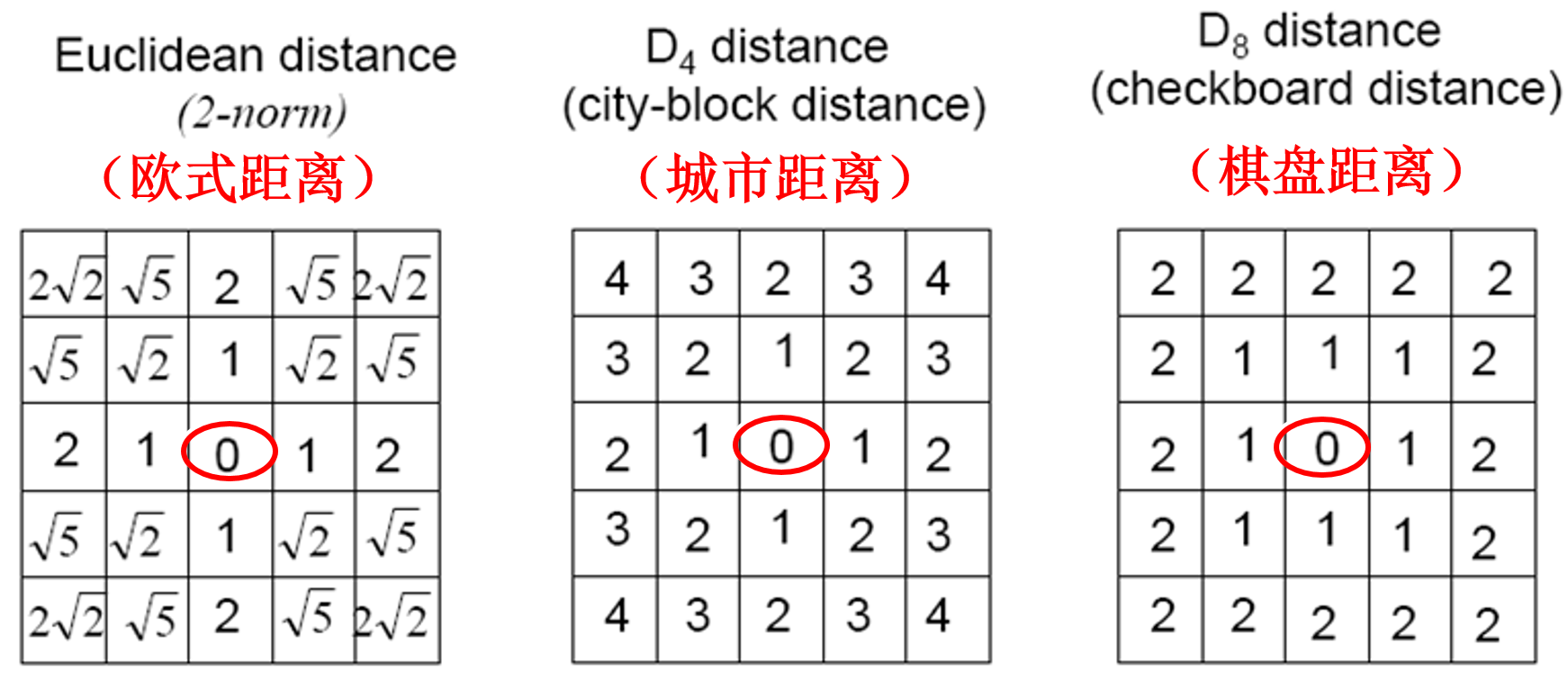
图2 三种邻域像素距离定义
矢量'g'的方向可以通过中心像素“z5” 相关邻域的单位矢量给出,这里的邻域是对称出现的,即四个方向对: (z1, z9) ,(z2, z8), (z3, z7), (z6, z4)。沿着4个方向对上求其梯度矢量和,可以给出当前像素(z5)的平均梯度估计,则有
G = (z3-z7)/4 * [1, 1]+ (z1-z9)/4 * [-1, 1]+ (z2-z8)/2 * [0, 1]+ (z6-z4)/2 * [1, 0]
式中, 4个单位向量 [1, 1],[-1, 1],[0, 1], [1, 0] 控制差分的方向,系数1/4, 1/2为距离反比权重。
上式展开后,有
G = [(z3- z7- z1+ z9)/4 + (z6-z4)/2, (z3- z7+ z1- z9)/4 + (z2-z8)/2]
注意,上述公式里并没有求平方根。如果要求数字上的精确度,上式需要除以4得到平均梯度值。然而,一些典型的运算都是针对数值较小的整数的定点运算,除法会丢失低阶的重要字节, 更方便的是把向量乘于4,而不是除于4,以保留低阶字节。因此,计算出的估计值比平均梯度在数值上扩大了16倍。
这样,计算公式变为:
G' = 4*G
= [z3 - z7- z1+ z9 + 2*( z6 - z4), z3 - z7 + z1- z9 + 2*( z2-z8)]
= [z3 + 2*z6 + z9 - z1 - 2*z4-z7, z1 + 2*z2 + z3 - z7 - 2*z8 - z9]
按x-y方向,可分别写成:
G'x = (z3 + 2*z6 + z9) - (z1 + 2*z4 + z7)
G'y = (z1 + 2*z2 + z3) - (z7 + 2*z8 + z9)
以上式子,就与我们教科书上的表达式完全一致了,也很容易得出如图1所示的两方向Sobel算子模板。在邻域像素距离模型上,如果改用欧式距离,就不难得到Frei和Chen(1991)提出的边缘检测器了[3]。
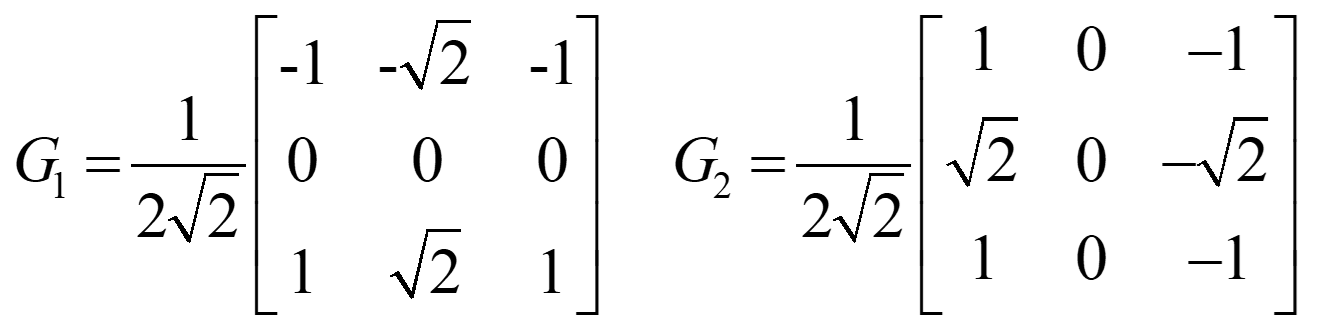
另外,教科书上的一些经典滤波器,其实也都有它的计算模型,而不是人为的随意构建,如高斯(Gaussian)滤波器,拉普拉斯(Laplacian)滤波器,LoG滤波器等。
写这篇文章,是因为4年前写了一篇博文:作者40年后谈Sobel算子的由来和定义[4]。博文下有匿名博主留言说没有看懂原理描述,本文可作为先前博文的补充和对匿名留言的回复。
同时,作为一个授课教师,也应该对这些算子或滤波器的数学基础和模型原理有更深入的理解,不能给学生打马虎眼。
参考阅读
[1] Sobel I, Feldman G., A 3x3 isotropic gradient operator for image processing[C], A talk at the Stanford Artificial Project in 1968, 271-272.
[2] https://www.researchgate.net/publication/239398674_An_Isotropic_3_3_Image_Gradient_Operator.
[3] http://rastergrid.com/blog/2011/01/frei-chen-edge-detector/.
[4] 彭真明,作者40年后谈Sobel算子的由来和定义,http://blog.sciencenet.cn/blog-425437-776050.html.

长按/扫一扫二维码,敬请关注“闻道研学” !