一幅图像f的空域拉普拉斯(Laplacian)算子如下式(1),即:

利用傅里叶变换的微分性质,可以推导出对应的频域Laplacian滤波器如下式(2),即

其中,u = 0,1,2,…,M-1; v = 0,1,2,…,N-1,为频率变量。M, N为输入图像f的尺寸。
对应的中心化滤波器如下式(3):
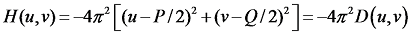
其中,P, Q 为滤波器H的尺寸。一般取,P = 2M, Q = 2N。
要实现图像f的锐化,需对f做傅里叶变换,然后利用H进行频域Laplacian滤波,按以下式(4)反变换求得其空域Laplacian图,即
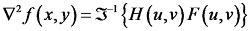
其中,F(u,v)为输入图像f(x,y)的傅里叶变换,符号Ξ-1代表傅里叶反变换。
按以下式(5),将傅里叶反变换得到的Laplacian图叠加于原始图像f,即

因▽2f(x,y)存在负值,故取c=-1,从而实现对原始图像f的锐化。由于Laplacian滤波结果存在黑、白两类轮廓细节,这样做主要是强化弱边缘,弱化了强边缘,使得锐化图像看起来比较自然,更适合于人眼观察。
Laplacian锐化的本质,即在原图像上叠加Laplacian滤波的高频(细节)成分,使得图像边缘轮廓更清晰。
尽管以上原理看似很简单, 所有教材上也都是这么表述的。但真正自己编写程序代码实现时,还是问题不少。主要表现在以下三个环节:
1)傅里叶反变换得到▽2f(x,y)的值的数量级要比f大几个数量级,因此,存在比例缩放(Scaling)问题。
2)叠加高频细节后的图g,改变了原始f的值域范围,并同样存在负值。如果对g简单使用归一化处理,将最小值映射为0,最大值映射为1,可能会改变整幅图像g的对比度,显示时看起来整个图将变暗(与输入图像f对比)。这并不是我们期望看到的结果。
3)频域滤波中会出现边界效应,导致图像的边界也会被锐化。
解决以上三个问题的对应办法是:
1)傅里叶变换前,对f先做归一化处理,使f的值的范围在[0,1];把式(4)求得的Laplacian结果除它(或绝对值)的最大值max(▽2f(x,y)),使得其值控制在[-1,1]范围。这样,二者才具有数值上的可比性。
2)因f和▽2f(x,y)的叠加结果还可能超过[0,1]范围,强制类型转换或归一化到[0,1],会使锐化结果整体变亮或变暗。有效的措施,就是利用原始图像f的实际灰度值范围[min(f) max(f)]对锐化结果g进行标定(Scaling),再次调整其灰度范围,使它保持与f基本一致。
3)关于边界的处理问题,请参考前述博文(见:如何保持空域与频域滤波结果的一致性)。只不过直接从频域定义H,无法对应空域h的尺寸,一般对f进行边界的扩充时,适当增加重复边界数,可以得到比较理想的处理结果。因为重复('replicate')边界像素,不会产生额外边缘。
以上为正确实现频域锐化的关键问题及相应的解决措施。对于空域Laplacian锐化,尽管用于叠加的高频成分与原始图像灰度的量级相差要小一些,但要得到好的锐化效果,同样也存在以上问题。
以下是对输入的模糊moon图像分别进行Laplacian空域(图1)和频域(图2)锐化的结果。可以看出,空间域和频率域的锐化结果基本一致。若频域滤波器H由空域模板h计算产生,则锐化结果的一致性会更好。
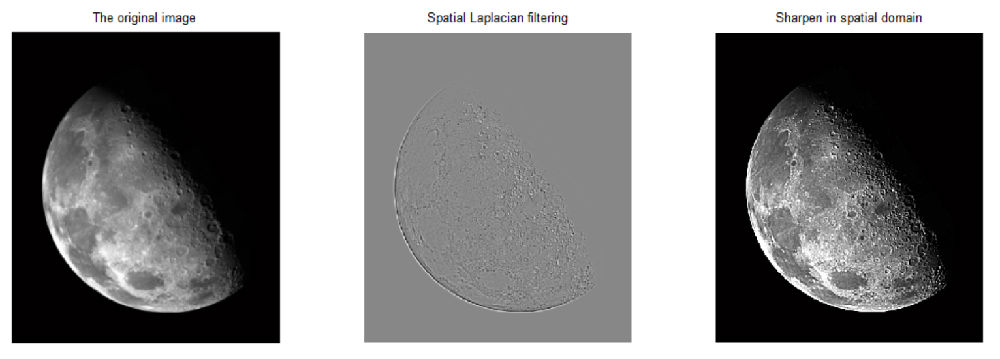
图1 空域Laplacian滤波及锐化结果

图2 频域Laplacian滤波及锐化结果
根据以上原理实现图像锐化的MATLAB代码,请下载:myimlapsharp.rar


扫一扫,可关注“老马迷图”微信公众号!
相关博文:如何保持空域与频域滤波结果的一致性(续)