现实系统多由大量相互作用的个体所构成，将这些真实系统抽象成复杂网络[1]，那么现实世界中的很多传播现象均可以抽象为复杂网络上的传播动力学[2-4]，其中，信息传播处处可见，例如防疫信息的宣传，创新技术的推广，谣言和商业广告的扩散等。如何促进有价值信息的传播，既是方法论上的挑战，又具有重要的现实意义。

在复杂网络系统中，信息通过节点之间的连边进行传播。网络连边在信息传播过程中起到了关键性的作用。真实网络往往庞大而稀疏，通过人为在原网络中增加一条或者多条连边，可以促进网络上信息的传播。鉴于此，我们在传统的易感态-已知态-恢复态（Susceptible-Informed-Recovered，SIR）信息传播模型[5-6]基础之上（该模型和我们常见的Susceptible-Infected-Removed模型动力学机制是一致的），提出了一个有效的基于连边的信息传播促进策略。

具体来说，我们首先通过分析SIR模型的演化规律，发展了一套SIR模型的边状态方程分析方法。利用SIR模型的边状态方程可以快速地确定信息传播的最终状态。图1展示了不同有效传播概率β所对应的信息最终传播范围ρ。其中，实线代表迭代SIR模型的边状态方程得到的最终传播范围，而空心圆代表通过蒙特卡洛仿真得到的最终传播范围。图1中的结果证明了通过迭代SIR模型的边状态方程可以准确地预测信息的最终传播范围。

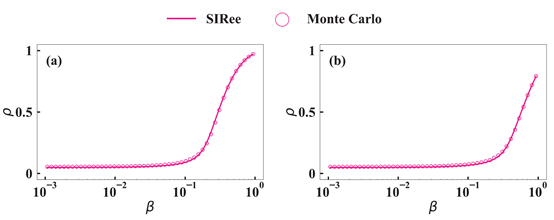
图 1 边状态方程迭代结果与蒙特卡洛仿真结果的比较

基于此，我们提出了一个潜在连边的影响力指标。结合SIR模型的边状态方程，该指标可以定量刻画在原网络中增加每条潜在连边（潜在连边指在原网络中不存在的连边）对信息传播的影响力，从而帮助我们确定能促进信息传播的最优潜在连边。最后，我们依次在原网络中增加最优潜在连边以达到促进信息传播的目的。注意每次增加了一条连边之后，都要重新计算每条潜在连边的影响力指标。

为了验证我们所提出的策略的优越性，我们将其与其它三个启发式的对比策略进行比较。这三个对比策略分别是：1）度乘积策略，即依次在度乘积最大的两个节点之间增加连边，且每增加一条连边后均要重新计算每条潜在连边对应的节点度乘积；2）特征向量乘积策略，即依次在特征向量乘积最大的两个节点之间增加连边，且每增加一条连边后均要重新计算每条潜在连边对应的节点特征向量乘积；3）随机策略，即每次都随机挑选两个不相连的节点，然后在它们之间增加连边。图2展示了利用不同策略在9个真实网络中增加N/2（N为网络节点数）条连边后信息最终传播范围的增量。其中，粉红色的实线代表我们提出的策略；橘色的短划线代表度乘积策略；绿色的点线代表特征向量乘积策略；黄色的点划线代表随机策略。实验结果表明，在一般参数条件下，我们的策略可以有效地促进网络中的信息传播，且效果优于其它的启发式对比策略。

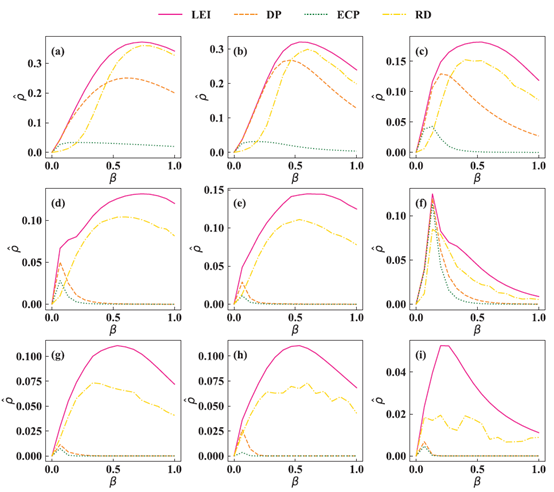
图 2 不同策略的效果对比。

我们所提出的基于连边的信息传播促进策略，有效地结合了网络结构信息和传播动力学信息，提供了一种研究信息传播促进策略的新思路。同时，我们的理论研究也可以为现实生活中促进防疫信息的宣传，创新技术的推广和商业广告的扩散等提供决策支持。

论文信息：D. Yang, J. Xian, L. Pan, W. Wang, T. Zhou, Effective Edge-Based Approach for Promoting the Spreading of Information, IEEE Access 8 (2020) 83745-83753.

论文PDF

Effective Edge-Based Approach for Promoting the Spreading of Information.pdf

免费下载地址：http://doi.org/10.1109/ACCESS.2020.2992058

参考文献：

[1] M. E. J. Newman. Networks[M]. Oxford, UK: Oxford University Press, 2018

[2] G. E. Kreindler, H. P. Young. Rapid innovation diffusion in social networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2014, 111: 10881-10888

[3] L. Laranjo, A. Arguel, A. L. Neves, et al. The influence of social networking sites on health behavior change: A systematic review and meta-analysis[J]. Journal of the American Medical Informatics Association, 2014, 22(1): 243-256

[4] P. Wang, M. C. González, C. A. Hidalgo, et al. Understanding the spreading patterns of mobile phone viruses[J]. Science, 2009, 324(5930): 1071-1076

[5] A.-L. Barabási. Network science[M]. New York, NY, USA: Cambridge University Press, 2016

[6] Z. K. Zhang, C. Liu, X. X. Zhan, et al. Dynamics of information diffusion and its applications on complex networks. Physics Reports, 2016, 651: 1-34.