我们知道,快速傅里叶变换(FFT)是信号处理的重要数学工具。一般而言,n点信号的离散傅里叶变换(DFT)的变换结果(频域)也是n个数据点。但在实际应用中,对实际信号作FFT 时,常常涉及到变换前数据需要补零(Zero padding)的问题。一些论坛里,曾看到某些专业人士从信息论的角度分析认为:“Zero padding没有增加时域信号的有效信息,因此,不会改变DFT/FFT的分辨率”。那么,补零到底有什么用,什么时候需要补零呢?对于一般的工程技术人员来说,基本就是调用现成代码或模块进行计算,很少考虑这些问题。其实,了解和搞清楚这个问题,对实际应用还是很有帮助的。接下来,我们将从以下几个方面来简要阐述如何补零以及它对频谱分析结果的影响。
一、什么是补零(Zero Padding)?
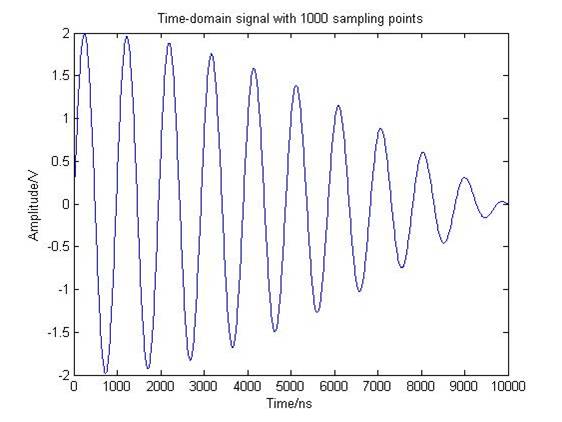
简单来说,补零(Zero Padding)就是对变换前的时域或空域信号的尾部添加若干个0,以增加数据长度。如图1所示,为含有1.00 MHz 和1.05 MHz 两个频率成分合成的正弦波实信号。
(a)
(b)
图1 时域信号的补零示意图
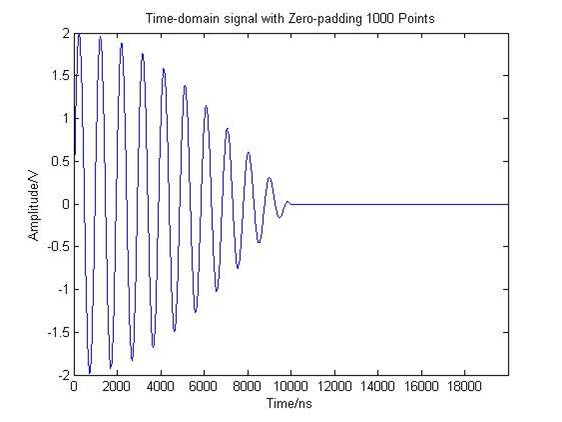
图1(a)中信号长度为1000个样点,采样频率为fs=100 MHz时,信号的实际时长则为10 us。在其尾部添加1000个0,即数据增加到了2000个点(时长为20us),则变为图1(b)所示的波形。
这个过程就是通常所说的补零(Zero Padding)。
二、为什么要Zero Padding?
最直接的理由就是,如果时域波形的数据样点为2的整数幂的话,FFT计算将是最高效的,硬件(FPGAs)计算FFT,就是采用了这样的Padding工作模式。那么,我们所关心的补零会不会影响计算输出的频率分辨率呢。
三、关于FFT频率分辨率
这里涉及到两种意义下的分辨率问题,一种叫“波形频率分辨率(Waveform frequency resolution”)或叫视觉频率分辨率(Visual frequency resolution);另一种则叫做“FFT分辨率”。虽然,这个分类和命名不一定是很专业的术语,但却有助于对“频率分辨率”概念的理解。在没有补零的情况下,这两个概念通常容易被混淆,因为它们是等价的。
波形频率分辨率是指可以被分辨的2个频率的最小间隔(Spacing);而FFT 分辨率则是频谱中的数据点数(The number of points in the spectrum),它是与做FFT的点数直接相关的。
因此,波形频率分辨率可定义为:
ΔRw= 1/T 7
其中,T是实际信号的时间长度。
同样,FFT分辨率可以定义为:
ΔRf= fs/Nfft
其中,fs为采样频率(the sampling frequency),Nfft为FFT的点数。ΔRf代表了FFT频率轴上的频率取值的间隔(Spacing)。
值得注意的是,可能有很好的FFT分辨率,但却不一定能够很好的把2个频率成分简单的分开。同样,可能有很高的波形分辨率,但波形的能量峰值会通过整个频谱而分散开(这是因为FFT的频率泄漏现象)。
我们知道,信号的离散傅里叶变换(DFT)或快速傅里叶变换(FFT)是对波形的任何一边补零形成的无限序列进行计算的。这就是,为什么FFT的每个频率单元(bin)都具有明显的sinc 波的形状。
波形频率分辨率1/T与一个sinc函数空值间隔(the space between nulls)是一样的。
四、例析
下面以一个具有2种频率成分的周期信号为例,说明Zero Padding与频谱分辨率的关系:
x = sin(2*pi*1000000*t)+sin(2*pi*1050000*t)
其中,f1 = 1.00MHz,f2 = 1.05MHz,频率间隔为0.05MHz。也就是说,在我们的频谱分析曲线上能看到2个频率点的峰,若2个正弦波的幅度为1伏( V),那么我们期望在1 MHz 和 1.05 MHz的频率点处的功率为10 dBm。
分以下几种情况进行分析:
1)时域信号1000个点采样,做相同样点数的FFT
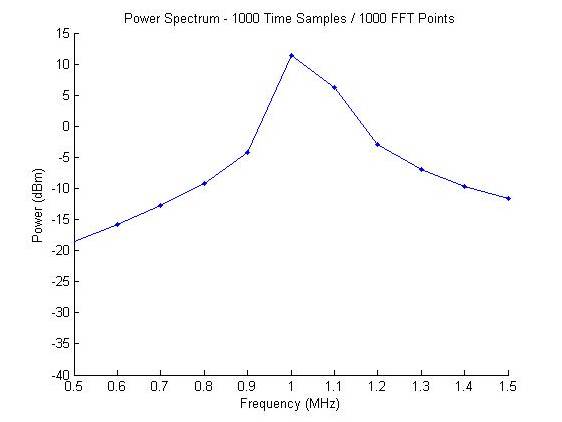
图2 原始信号的功率谱(1000点 FFT)
图2中,我们并没有看见期望的两个脉冲,因为图中仅出现一个脉冲点,其幅度约为11.4 dBm。显然,这个图并不是我们想要的正确的频谱图。原因很简单,没有足够的分辨率看见两个峰值(Peaks)。
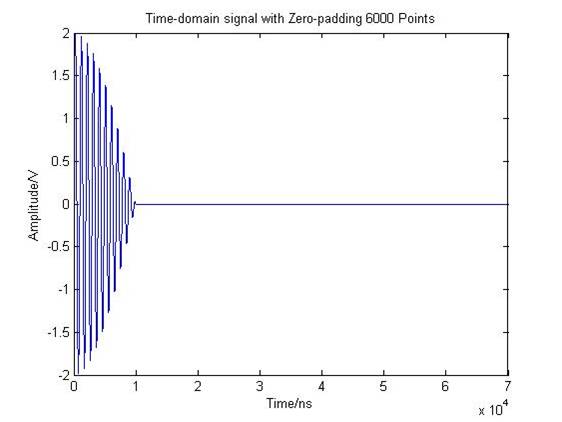
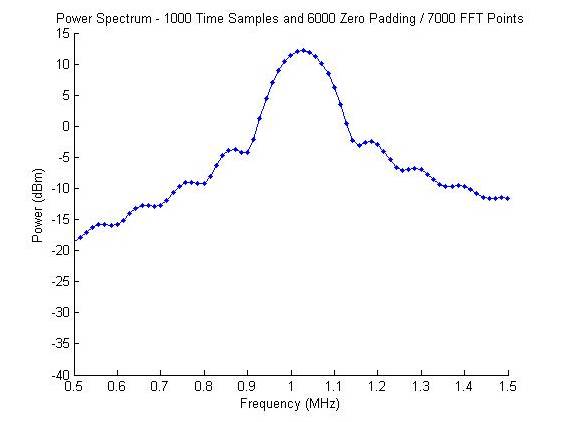
2)时域信号1000个点采样,后端补6000个零,做7000点数的FFT
我们自然想到,采用补零方式增加FFT点数,以使频率轴上能增加更多点数。如采用7000个点做FFT,即需要在原1000点信号尾部增加6000个零值(即60us时长),则原始信号变为图3(a)所示,其FFT结果如图3(b)所示。
(a)
(b)
图3 原始信号补零及功率谱(7000点 FFT)
图3中,我们也并没有看见期望的结果。仔细观察一下,此图到底告诉了我们什么呢?即通过增加更多FFT点数的做法,使得波形频率分辨率公式中的sinc函数的定义更清晰。可以看出,sinc 空值(nulls)间隔大约是0.1 MHz。
由于给出信号的两个正弦波的频率间隔是按0.05 MHz分隔的, 因此,不管我们用多少FFT点数(Zero padding),都无法解决2个正弦波的问题。
再来看一下频率分辨率ΔRf告诉了我们什么。尽管,FFT分辨率大约为14kHz(足够的频率分辨率), 而波形频率分辨率仅仅为100 kHz。两个信号的频率间隔是50kHz,所以我们受限于波形频率分辨率ΔRw。
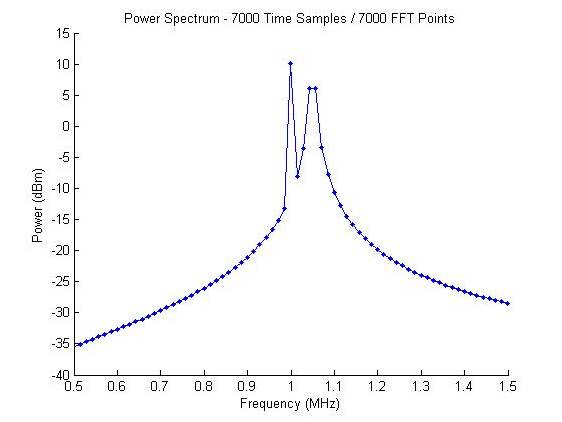
3)时域信号7000个点采样,做7000点数的FFT
为了合理地解决这个频谱的问题,需要增加用于FFT的时域数据的长度(点数)。因此,我们直接采集波形的7000点作为输入信号,取代补零(Zero Padding)方式到 70us (7000 点) 。时间域信号及对应的功率谱分别如图4a-4b所示。

(a)
(b)
图4 按7000点采集的信号及其功率谱
通过时域数据的周期延拓,现在的波形频率分辨率ΔRw也近似为14KHz。但从频谱图中,我们还是看不见2个正弦波。1 MHz 信号已按正确的10 dBm功率值清晰地表征,而1.05 MHz 信号变宽,且未以期望的10 dBm 功率分布。这是为什么呢?
原因就是1.05 MHz处并没有FFT点的分布,原因是此处的能量被多个FFT点分散(泄露)了。
给出的例子中,采样频率是100 MHz,FFT点数为7000。频谱图中,点与点之间的间隔是14.28 kHz。1 MHz频率刚好为频率间隔的整数陪,而1.05 MHz 却不是。距1.05 MHz最近的整数倍频率为1.043 MHz 和1.057 MHz, 因此,能量被这2个FFT单元所分散。
4)时域信号7000个点采样,后端补1000个零,做8000点数的FFT。
为了解决这个问题,我们可以合理选择FFT的点数,以便这两个点能在频率轴上成为独立分开的点。由于,我们并不需要更好的波形频率分辨率,仅采用时域数据的零填充方式来调整FFT数据点的频率间隔。
给时域信号增加1000零值(10 us),使得频率间隔为12.5 kHz,这样,满足了1 MHz and 1.05 MHz两个频率都是这个间隔的整数倍。此时,给出的功率谱如图5所示。可以看出,两个频率问题得到解决,而且功率均在期望的10 dBm。

图5 补零至8000点信号的功率谱
为了进一步观察过度补零的现象,通过时域补更多的零值(10000点)来完成更多点数的FFT(确保具有正确的波形频率分辨率ΔRw),我们就可以清晰地看到FFT单元(bins)的sinc波形状,如图6所示。
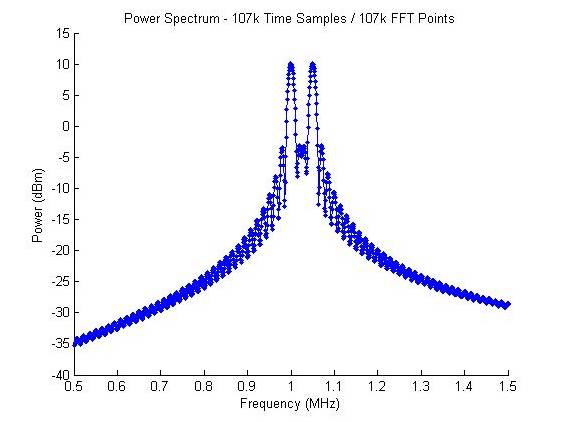
图6 补零至107000点信号的功率谱
博文中计算结果和图件,均利用MATLAB进行仿真验证。如需代码,可直接联系本人。
参考资料:http://www.bitweenie.com/listings/fft-zero-padding/

本博客内容与“老马迷图”个人微信公众号同步发布。欢迎关注!

扫一扫,可关注“老马迷图”微信公众号!
相关博文:
[2]三页PPT一堂课