本学期给学院的“卓越工程师计划”班本科生讲授一门“光电图像处理”课程。由于班级只有23个同学,上课能整点小改革,课堂上不必循规蹈矩,可以自由发挥。
与普通班上课不一样的是,我要求人人都带笔记本电脑进课堂(若直接在机房上课,就不存在这问题)。因为,这是一门图像处理课,仅推推公式,动动嘴皮还没用,必须教会学生利用计算机做数据处理。
开学这么久了,印象比较深的一堂课,就是上周五下午的一次课,2学时只讲了3页PPT,核心内容就1页PPT。
这章内容为图像变换及应用,其核心是傅立叶变换和频域滤波。说到傅立叶变换,大伙都不会陌生,不就是一个频谱分析的工具嘛,一个老掉牙的东东。这玩艺,忒容易!对于大三学生,信号与系统课程都是学过的。给一函数,一般都会根据公式计算变换结果。其实不然,对于数字(离散)信号傅立叶变换(DFT)的计算、编程实现、实现中的问题、变换结果的图形展示及物理意义的解释,不是所有人都是清楚的,甚至包括一些讲课老师。
如果对1-D DFT都不清楚的话,直接讲2-D图像的傅立叶变换,学生理解起来就困难了。以往,我也觉得这很简单。后来发现,课上完了,除了会调用现成的MATLAB函数做计算外,大部分同学却不会解释图像的频谱。因此,正式讲解图像的傅立叶变换前,有必要补充一下1-D DFT的内容。
以下是本次课的三张PPT。

第一张PPT,直接贴出DFT的正、反变换公式。简单解释变量的意义,大约3分钟时间。接着进入第二张PPT。
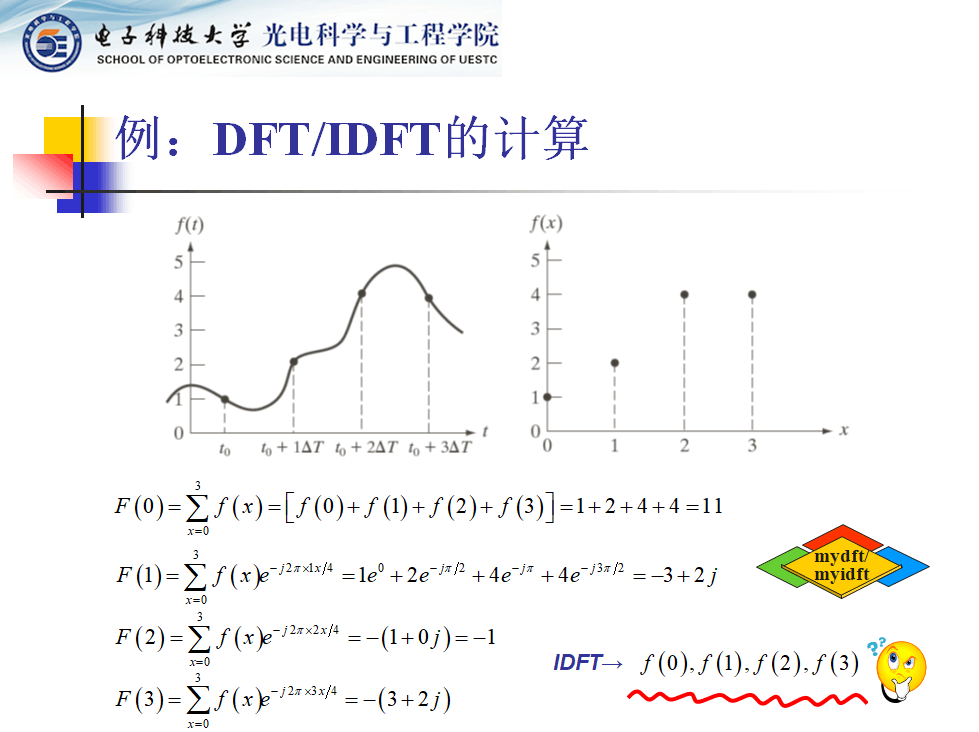
第二张PPT,其实就是布置给学生的课堂练习。PPT是先后播放的,最开始只有上面的2张图出现。所有学生自己手算完成正、反变换。给学生5分钟时间计算,最后给出正确答案。
如果数据点多了,手算是一件麻烦的事情。接着,根据第一张PPT上的DFT计算公式就可引入一段自行编写的mydft(x)的MATLAB函数代码。
function y = mydft(x)
%==============================================================================
% function: y = mydft(x)
% y is the discrete Fourier transform of acolumn n-vector x.
%==============================================================================
N = length(x);
for u=1:N
y(u)=0;
for n=1:N
y(u)=y(u)+x(n)*exp(((-1i)*2*pi*(n-1)*(u-1))/N);
end
end
调用以上mydft(x)函数代码(注:反变换myidft代码仅需修改2处,一处是虚数i前的-1改为+1;另外就是循环完成后,y=y/N),代替手算完成第二张PPT图的同样计算。
仅仅知道利用公式计算几个离散数据点的DFT,就是一种数学游戏,看不出这个工具到底有啥用,而且输入实数序列,输出变成了复数序列,更是不好理解了。
接下来,进入第三张PPT,一种预先知道频率成分的连续信号的DFT计算及其结果分析。
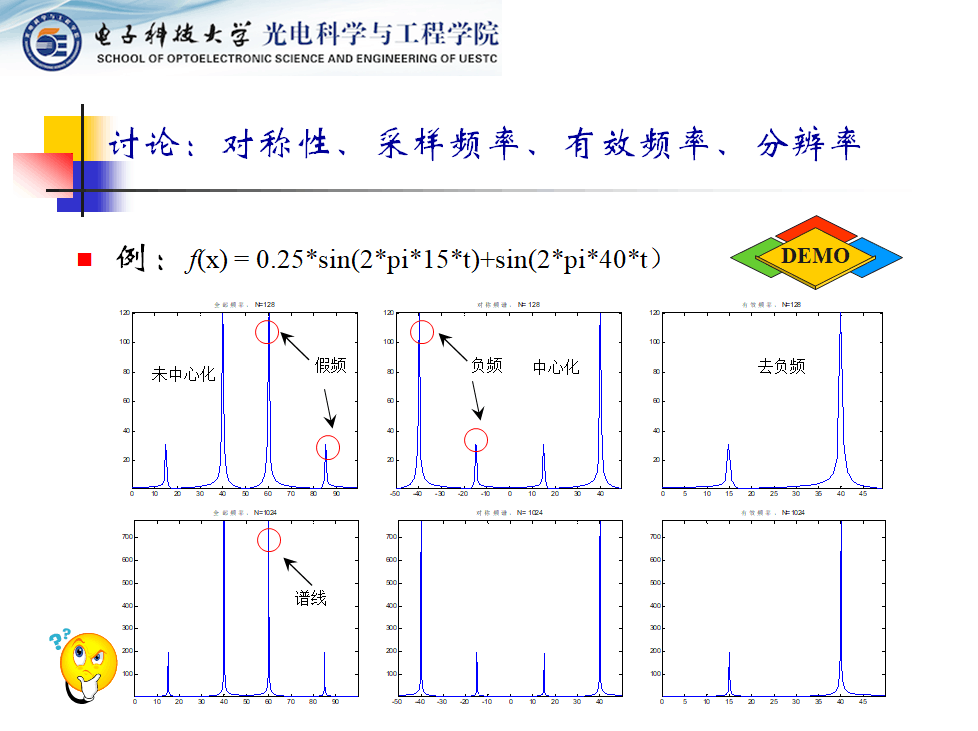
这张PPT主要以提问题、讨论及代码演示结合等方式进行。
1. 以上实例信号是连续信号还是离散信号?(提问)
2. 信号含有几个频率成分,分别是多少Hz?每个成分所占比例有什么不一样?(提问)
3. 这是频率稳定信号,还是非平稳信号?(提问)
4. 这个信号是否周期信号,如何确定它的周期?具体周期是多少?(提问)
空口无凭,眼见才为实。以下开始MATLAB代码的演示和讨论。
1)画出这个信号单个周期内的曲线。这过程会涉及到离散采样的问题,可以顺带回顾一下采样定理。特别地,要强调一下采样时间△t与采样频率fs的关系(如fs=100Hz,△t=1/fs)。
2)代码演示DFT计算(也可直接调用fft函数),求幅度,画出第一个图(左上)。解释图的意义,并说明直接计算出现视觉假频的原因。
3)代码演示DFT计算中频谱中心化问题(中上)。
4)第3)步中去掉负频(右上),便于实际信号频谱的解释。这里要留下问题,负频是不是没有意义?
5)改变频率轴采样间隔,做出与上一排相对应的三个图(下排)。对结果的解释:即采样频率fs保持不变的情况下,频率间隔密集了(△f↓),可以改善频谱绘制的(谱线)精细程度,提高视觉分辨率。
最后留下10-15分钟,学生自己动手编写代码,分别实现一个方波信号和实际音频信号的离散傅立叶变换(DFT),并画出相应的频谱。
这堂课,虽仅3页PPT,配合板书和代码演示。最后,学生的收获是很大的,并为下一节图像的离散傅立叶变换和频域滤波做了很好的铺垫。
相关博文:十年磨一“课”