最近Nowak等人指出，演化博弈模型中会出现某种非稳定现象，其时系统会很长时间处于几乎全是合作者的状态，然后突然出现大量背叛者，但是只持续很短时间，又会回到全部是合作者的情况。其实10年以前Beom Jun Kim就指出hub节点或者说意见领袖的存在会导致演化博弈中出现非稳定性。Nowak等人认为这种非稳定性和网络结构息息相关，并且在这种状态下系统总体收益很高。

我们的工作是希望像剥洋葱一下分离导致非稳定性的根本原因。

首先我们注意到即便不考虑任何网络结构和博弈模型，只考虑模拟和变异，就会变成一个Moran过程的变体，这个时候Nowak等人所观察到的非稳定性的主要特征就都齐备了。

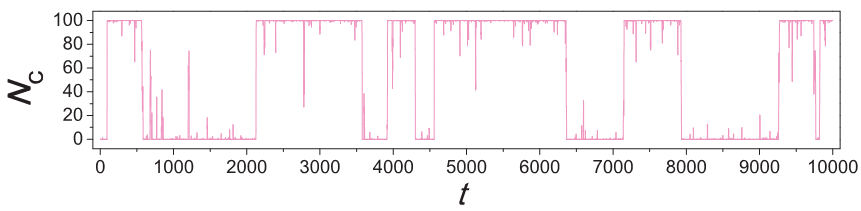
[完全不考虑博弈规则的一种变体的Moran过程，也可以观察到非稳定性，可以完全可以精确求解]

在囚徒博弈和雪堆中都观察到了这种非稳定性，博弈的具体规则主要是导致了非对称的出现。

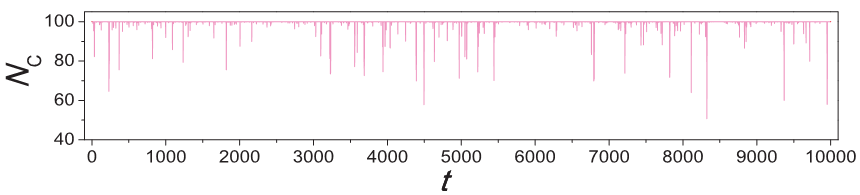
[博弈规则只是破坏对称性，并不影响失稳性]

至于网络结构嘛，不管是全连通的网络还是稀疏连接，又或者优先连接，都几乎不影响这种非稳定性。至少可以说，网络结构的作用较小。

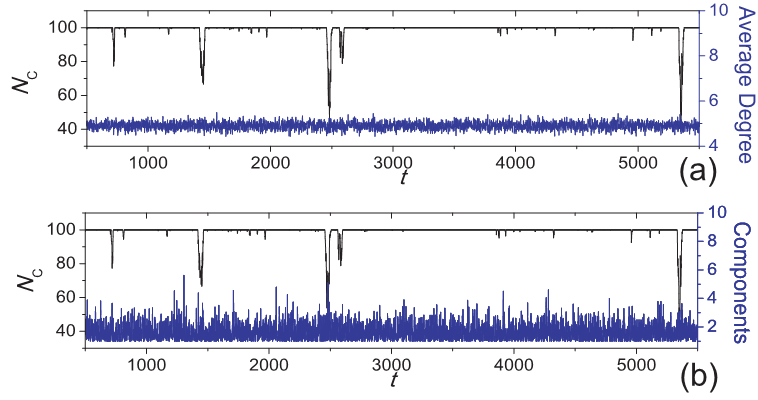
[出现失稳的时候网络结构岿然不动，这和Nowak的文章恰恰相反]

这篇文章是比较典型的慢慢剥洋葱的工作，它的解析比较干净（几乎所有结果都给出了解析），另外就是提出了一种度量非稳定性程度的方法（在这个工作尚不成熟的时候，我做过一个报告，当时樊瑛姐强烈建议我们提出一个这样的指标），这些都是可以一看的。上面提到的若干相关工作，论文中都有引用。这篇文章的另外三位作者是电子科技大学杨紫陌、香港中文大学许伯铭和温州大学柯见洪，非常感谢这三位合作者。

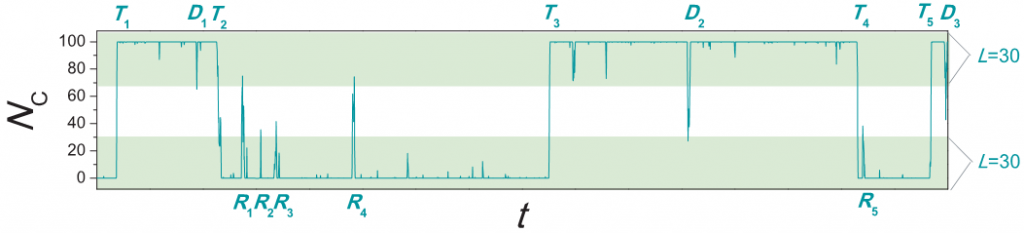
[我们提出了一种还不算成熟的度量非稳定性程度的方法，细节见论文]

论文信息：Zimo Yang, Tao Zhou, Pak-Ming Hui, Jian-Hong Ke, “Instability in Evolutionary Game”, PLoS ONE 7 (2012) e49663.

论文链接：http://www.plosone.org/article/info%3Adoi%2F10.1371%2Fjournal.pone.0049663

全文下载：