我们知道,给定一个空(时)间滤波器,既可以在空(时)域直接完成数字信号的滤波,也可以在频域完成。空域滤波的数学运算为卷积/相关,对应频域则为点乘/频域数据的共轭(G*)与滤波器(H)的乘积。
简单起见,以一个1D数字信号为例加以说明。
例如:给定信号x = [1 2 2 4 4],滤波器h = [1 2 3];
空域滤波(卷积)为:
y = conv(x,h,’same’); % 此处未考虑h系数的归一化问题
则滤波结果为:
y = [4 9 14 18 20]
下面介绍频域方式的滤波过程。由于时域滤波属于有限序列的线性卷积,频域滤波方式实际上是利用离散傅里叶变换(DFT)求时域线性卷积的过程,而DFT本质上是对应时域滤波中针对周期序列的循环卷积。要满足循环卷积与线性卷积计算结果一致,时域信号x(m点)与滤波器h(n点)必须等长。这可以采用补零的方法,使x与h的长度均为L≥m+n–1。这样做的目的,也是为了避免周期函数卷积中因周期靠近引起所谓的频率缠绕错误(混叠)。
一般做法是,对空(时)域数据采用后端补0方式延拓至2倍数据长度。
信号延拓: xp = [1 2 2 4 4 0 0 0 0 0];
由于滤波器h与延拓后的信号xp应保持相同的长度,故也需要补0做延拓。有两种方式:
(1) 双边延拓,滤波器h居中
hp = [0 0 0 0 1 2 3 0 0 0];
(2) 单边延拓,滤波器h居左
hp = [1 2 3 0 0 0 0 0 0 0];
然后,分别对xp,hp做DFT,完成频域滤波并做反变换,即
y = real(ifft(fft(xp).*fft(hp)));
最后,剪裁掉补0多出的后半部分数据,即保留主值序列。则两种方式得到的滤波结果分别为:
y1 = y(1:5) = [12 0 0 0 1]; 和 y2 = y(1:5) = [1 4 9 14 18];
可以看出,第一种延拓,滤波结果与空域结果完全不一致。第二种延拓与空域结果基本一致,但在左右短点处(边界部分)是不一致的。这里,第二种延拓也等价于:
y = real(ifft(fft(x,10).*fft(h,10)));
从傅立叶变换的时域性质知道,两种延拓的频谱是一样的,但相位会发生变化。因此,第一种延拓(两端补零方式,h居中)是不可取的。第二种延拓与空域滤波结果基本一致,但边界上有差异。那么,如何消除这种边界差异,达到与空域考滤波完全一致的结果呢?
我们只要在滤波器h延拓方式上稍作改动,即把空域滤波器中心元素放到最前段(起始点),左端被挤出的元素顺序放在尾部,即所谓的循环移位(circularly shift)法,则有:
hp = [2 3 0 0 0 0 0 0 0 1];
再按以上的相同步骤进行滤波处理,可得:
y = [4 9 14 18 20];
频域滤波与空域滤波的结果就可完全保持一致。
假如,空域做的是相关运算来完成滤波,那么,只要滤波器旋转180度后,采取同样的0填充方式。
显然,以上方式很容易推广到二维情况。如果有以下二维滤波器,即一个计算y方向梯度的Sobel算子。

由于图像的模板运算默认为相关运算,而频域的乘积对应空域卷积。要达到一致性,以上滤波器需要上下颠倒,即旋转180度后(若为对称滤波器,可省此步),即

以上模板在频域进行点乘可对应h的相关运算。
若需要填充0方式扩大到10×10(根据滤波图像的尺寸而定),则填充方式为:


以上两种方式中,hp的填充方式会出现与空域滤波结果边界上的不一致,而hp'填充方式则可以解决这个问题。
道理很简单,因为空域模板运算的当前像素(原点)一般是在滤波模板的中心像素,即
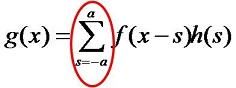
频域乘积(点乘)对应空域卷积的情况下,是按以下公式:
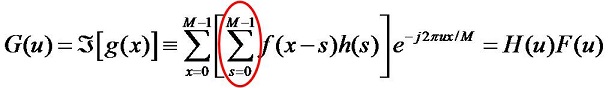
即原点(见椭圆标记处)是从左上角开始的。
下面的MATLAB代码可以简单实现以上方法,保持h中心像素位于填充区域的左上角。
center_h = ceil((size(h) + 1)/2); % 确定空域滤波器h中心像数坐标
hp = zeros(P, Q); % 生成P×Q的全零矩阵
hp(1:size(h,1), 1:size(h,2)) = h % 左上角填充h,形成延拓滤波器hp
row_indices = [center_h(1): P, 1: (center_h(1)-1)]';
col_indices = [center_h(2): Q, 1: (center_h(2)-1)]';
hp = hp(row_indices, col_indices); % 原点在左上角的延拓滤波器hp
其中,P, Q是扩充后的滤波器尺寸,与待处理图像(M×N)有关(一般取,P = 2M,Q = 2N)。以上代码也就是实现前面提到的滤波器h补零延拓+循环移位过程。
滤波器h补零延拓做FFT,虽然可以简单调用Hp = fft2(h,P,Q)来完成(MATLAB内部处理方式),但并未做循环移位,仅仅是右下部补零后计算FFT。因此,滤波结果的边界处并不能保证与空域滤波结果的一致性。空域滤波器h尺寸越大,这种边界差异越明显。例如用25×25,方差为2的空域高斯低通波器进行实验,结果如下。


上一排图分别为原图,空域滤波结果及模板置于左上角的频域滤波结果。可以看出,频域滤波结果有明显的边界效应。下图为模版中心像素置左上角的测试结果(右下图),则与空域滤波结果是完全一致的。
相关博文:如何保持空域与频域滤波结果的一致性(续)